ESTADÍSTICA DE LA PROBABILIDAD
Maria Johanna Angulo
Marta liliana Muñoz
Contaduría Publica
¿Qué es un diagrama de árbol?
El diagrama de árbol es una representación gráfica de los posibles resultados del experimento, el cual consta una serie de pasos, donde cada uno de los pasos tiene un número finito de maneras de ser llevado a cabo.
Se utiliza en los problemas de conteo y probabilidad.
¿Para qué sirve?
- Un diagrama de árbol es un método gráfico para identificar todas las partes necesarias para alcanzar algún objetivo final
- Se emplea para descomponer una meta u objetivo en una serie de actividades que deban o puedan hacerse. A través de la representación gráfica de actividades se facilita el entendimiento de las acciones que intervendrán
- Permite a los miembros del equipo de trabajo expandir su pensamiento al crear soluciones sin perder de vista el objetivo principal o los objetivos secundarios
- Ubica al equipo para que se dirija a situaciones reales versus teóricas.
Cómo se elabora
- Establezca el objetivo que se analizará a través del diagrama de árbol. Es muy importante que el objetivo quede claro para todos y que esté expresado de manera activa.
- Arme el equipo adecuado. Se sugiere un equipo de 4 a 8 participantes. Considere que aquellos que seleccione deberán estar involucrados en la problemática a fondo para aportar soluciones y que el diagrama de árbol cuente así con los niveles de análisis necesarios.
- Genere el mayor número posible de “cabeceras del diagrama de árbol” Esto es las ideas o sub-objetivos hacia los que se enfocarán las acciones para lograr el objetivo principal.
- Descomponga cada “cabecera” o título principal en mayor detalle. Vaya acomodando las ideas por subtemas llegando a tres o cuatro niveles.
- Detenga la descomposición de temas cuando ya se perfilen tareas específicas a realizarse.
- Revise el diagrama de árbol. Asegúrese de que tiene un flujo lógico y que esté lo más completo posible.
- Pregunte al equipo si observa algún punto que sea muy obvio y se haya olvidado incluir.
- Pregúntese junto con el equipo si las tareas resultantes son necesarias para lograr el objetivo.
Ventajas
- Exhorta a los integrantes del equipo a ampliar su modo de pensar al crear soluciones.
- Mantiene a todo el equipo vinculado a las metas y sub metas generales de una tarea.
- Mueve al equipo de planificación de la teoría al mundo real.
Beneficios
- Permite obtener una visión de conjunto del objeto de estudio.
- Permite identificar los medios necesarios para alcanzar una meta o resolver un problema.
- Permite identificar las causas primarias y secundarias de un problema y asignar prioridades al momento de resolver un problema.
- Permite entender la relación causa – efecto de los problemas.
- Permite identificar los objetivos las metas de cada tarea.
Fuentes: wikipedia.org / dgplades.salud.gob.mx / aiteco.com / articulo.org
Principio de la multiplicación.
“Si un suceso se puede realizar de “m” formas diferentes y luego se puede realizar otro suceso de “n” formas diferentes, el número total de formas en que pueden el otro. El “y” indica multiplicación.
Ejemplo: ¿de cuántas formas se puede vestir una persona que tiene 3 pantalones y 3 camisas?
Para vestirse, la persona se pone el pantalón y luego la camisa, es decir tiene 3 x 3 = 9 opciones diferentes de vestirse.
Si se desea llevar a efecto una actividad, la cuál tiene formas alternativas para ser realizada, donde la primera de esas alternativas puede ser realizada de M maneras o formas, la segunda alternativa puede realizarse de N maneras o formas ..... y la última de las alternativas puede ser realizada de W maneras o formas, entonces esa actividad puede ser llevada a cabo de,
M + N + .........+ W maneras o formas
Ejemplos:
1) Una persona desea comprar una lavadora de ropa, para lo cuál ha pensado que puede seleccionar de entre las marcas Whirpool, Easy y General Electric, cuando acude a hacer la compra se encuentra que la lavadora de la marca W se presenta en dos tipos de carga ( 8 u 11 kilogramos), en cuatro colores diferentes y puede ser automática o semiautomática, mientras que la lavadora de la marca E, se presenta en tres tipos de carga (8, 11 o 15 kilogramos), en dos colores diferentes y puede ser automática o semiautomática y la lavadora de la marca GE, se presenta en solo un tipo de carga, que es de 11 kilogramos, dos colores diferentes y solo hay semiautomática. ¿Cuántas maneras tiene esta persona de comprar una lavadora?
Solución:
Suponga que un salón de clase está constituido por 35 alumnos.
a) El maestro desea que tres de los alumnos lo ayuden en actividades tales como mantener el aula limpia o entregar material a los alumnos cuando a
M = Número de maneras de seleccionar una lavadora Whirpool
N = Número de maneras de seleccionar una lavadora de la marca Easy
W = Número de maneras de seleccionar una lavadora de la marca General Electric
M = 2 x 4 x 2 = 16 maneras
N = 3 x 2 x 2 = 12 maneras
W = 1 x 2 x 1 = 2 maneras
M + N + W = 16 + 12 + 2 = 30 maneras de seleccionar una lavadora
Permutaciones
Para entender lo que son las permutaciones es necesario definir lo que es una combinación y lo que es una permutación para establecer su diferencia y de esta manera entender claramente cuando es posible utilizar una combinación y cuando utilizar una permutación al momento de querer cuantificar los elementos de algún evento.
sí sea necesario.
b) El maestro desea que se nombre a los representantes del salón (Presidente, Secretario y Tesorero).
Solución:
a) Suponga que por unanimidad se ha elegido a Daniel, Arturo y a Rafael para limpiar el aula o entregar material, (aunque pudieron haberse seleccionado a Rafael, Daniel y a Enrique, o pudo haberse formado cualquier grupo de tres personas para realizar las actividades mencionadas anteriormente).
¿Es importante el orden como se selecciona a los elementos que forma el grupo de tres personas?
Reflexionando al respecto nos damos cuenta de que el orden en este caso no tiene importancia, ya que lo único que nos interesaría es el contenido de cada grupo, dicho de otra forma, ¿quiénes están en el grupo? Por tanto, este ejemplo es una combinación, quiere decir esto que las combinaciones nos permiten formar grupos o muestras de elementos en donde lo único que nos interesa es el contenido de los mismos
.
b) Suponga que se han nombrado como representantes del salón a Daniel como Presidente, a Arturo como secretario y a Rafael como tesorero, pero resulta que a alguien se le ocurre hacer algunos cambios, los que se muestran a continuación:
Combinaciones
Como ya se mencionó anteriormente, una combinación, es un arreglo de elementos en donde no nos interesa el lugar o posición que ocupan los mismos dentro del arreglo. En una combinación nos interesa formar grupos y el contenido de los mismos.
La fórmula para determinar el número de combinaciones es:
Ejemplo:
1) a. Si se cuenta con 14 alumnos que desean colaborar en una campaña pro limpieza del Tec, cuantos grupos de limpieza podrán formarse si se desea que consten de 5 alumnos cada uno de ellos, b.si entre los 14 alumnos hay 8 mujeres, ¿cuantos de los grupos de limpieza tendrán a 3 mujeres?, c.¿cuántos de los grupos de limpieza contarán con 4 hombres por lo menos?
Solución:
a. n = 14, r = 5
14C5 = 14! / (14 - 5 )!5! = 14! / 9!5!
= 14 x 13 x 12 x 11 x 10 x 9!/ 9!5!
= 2002 grupos
Entre los 2002 grupos de limpieza hay grupos que contienen solo hombres, grupos que contienen solo mujeres y grupos mixtos, con hombres y mujeres.
b. n = 14 (8 mujeres y 6 hombres), r = 5
probabilidades
1. un estudio sobre los gustos musicales
de los estudiantes en una universidad se encuesto
un total de 70 estudiantes quienes manifestaron sus gustos de la siguiente
manera:
|
||||||||||||||||
20 la música salsa
|
23 rock
|
40 baladas
|
10 baladas y salsa
|
|||||||||||||
13 baladas y rock
|
5 rock y salsa
|
3 rock , salsa, baladas
|
||||||||||||||
diagrama de venn
|
||||||||||||||||
70
|
||||||||||||||||
2. Un producto se arma en tres
etapas en la primera etapa hay 5 líneas
de armado en la segunda 4 líneas,
En la tercera 6 líneas
¿de cuantas formas puede moverse el producto en el proceso de armado?
|
||||||||||||||||
principio de la multiplicación
|
5*4*6=120
|
|||||||||||||||
3.en Colombia las placas de los carros están
formadas por tres números y tres letras :
|
||||||||||||||||
a. ¿cuántas placas se pueden generar en
estas condiciones?
Se
puede escoger de 10 maneras diferentes
así que :
|
||||||||||||||||
3 números
10*10*10*28*28*28=21952000
|
||||||||||||||||
b. En este experimento es válido hablar de
orden de muestra?
en este caso en particular no importa si se intercalan números y letras |
||||||||||||||||
c.
en caso que para una ciudad como Medellín se asignen solamente las placas cuya
primera letra es m o n ¿cuántos automóviles pueden estar matriculados en
Medellín?
10*10*10*2*28*28=1568000
4
. un vendedor de automóviles nuevos quiere impresionar a sus clientes potenciales con la cantidad posible de diferentes
combinaciones de que se disponen un modelo presenta tres tipos de motores, dos
trasmisiones , cinco colores de
carrocería y dos colores de interiores,
¿Cuántas posibilidades de elecciones
existen respecto a estas
opciones?.
Se
toman todas las opciones y se aplica
el principio de la multiplicación
3
tipos de motores * 2 trasmisiones* 5
colores de carrocerías* 2 colores de interiores
= 60 serian la cantidad de muestras.
5.
explique la diferencia entre:
PERMUTACIONES
|
COMBINACIONES
|
||||||||
*si
importa el orden
|
* no
importa el orden
|
||||||||
Calcula
las posibles agrupaciones que se pueden establecer con todos los elementos de
un grupo, por lo tanto, lo que diferencia a cada subgrupo del resto es el
orden de los elementos
|
Determina
el número de subgrupos de 1, 2, 3, etc. elementos que se pueden formar con
los "n" elementos de una nuestra
|
||||||||
Así
que en matemáticas usamos un lenguaje más preciso:
Una permutación es una
combinación ordenada.
|
|||||||||
6.
se juegan 5 dados ¿de cuantas maneras
pueden caer?
6 6 6 6 6 =7776
⧪* ⧪* ⧪ *⧪* ⧪
6 6 6 6 6 =7776
⧪* ⧪* ⧪ *⧪* ⧪
7.si
un conjunto tiene 10 elementos, ¿Cuántos
subconjuntos de 2 electos puedes formar si el orden en aparece en los 2
elementos tiene importancia.
aplicamos la formula.
nPr = _n!____
(n-r)!
=10Pr= 10!
_________ =_10! ___
(10-2)! 8!
=10*9*8! =90 formas
nPr = _n!____
(n-r)!
=10Pr= 10!
_________ =_10! ___
(10-2)! 8!
=10*9*8! =90 formas
8!
8) en un concurso de belleza se suele escoger 15 sefinalistas y luego se escogen 5 finalistas de cuantas diferentes formas se pueden ocupar 5 primeros puestos.
Solución:
Multiplicación de opciones.
Dando que M=15 Y N=5, hay 15*5=75 maneras distintas en que se pueden elegir las 5 finalistas.
9) una liga de futbol está integrada por 6 equipos, cuantos resultados diferentes posibles habrán en una temporada supón que ningún equipo terminada empatado con el otro.
SOLUCIÓN:
Puesto que n1=n2=n3=n4=n5=n6 en total hay.
6.6.6.6.6.6= 46656 posibilidades de resultados diferentes en la liga.
10. la junta de una compañía ABC ESTA COMPUESTA por 15 miembros de cuanta maneras se puede elegir un vicepresidente, presidente y secretario.
Dando que M=15 Y N=3, hay 15*3=45 maneras distintas en que se pueden elegir las un presidente, vicepresidente y un secretario.
11. se va a elegir un comité de 5 miembros entre un grupo de 7 candidatos de cuantas formas se puede hacer esto, si los 7 candidatos van a ocupar puestos diferentes. De cuantas maneras pueden ocupar estos puestos.
Solución
Puesto que n1= y n=7, hay 5*7= 35 formas de elegir 5 miembros del comité
12. en una clase de estadística hay 30 estudiantes 24 hombres y 6 mujeres de cuantas maneras se puede constituir un comité de cuatro estudiantes de cuantas maneras si debe haber 2 mujeres en el comité.
Solución
30 hombres dando que n1=30,n2=29, n3= 28 sin importar el orden a quien elija hay 30*29*28=24.360 posibilidades distintas.
6 mujeres dando que n1=6,n2=5,=4 sin importar el orden a quien elija hay 6*2= 12 posibilidades distintas.
13 un estudiante tiene 7 libros que quiere colocar en su biblioteca sin embargo solo caben 4 cuantas maneras existen para colocar solo 4 libros
Solución
Conjuntos
Conjunto (del
latín coniunctus) es lo que está unido, contiguo o incorporado a otra cosa, o que se encuentra mezclado, combinado o aliado con
otra cosa diversa. Un conjunto, por lo tanto, es un agregado varias cosas o personas.
Ejemplo
Conjunto de los números primos”.
Complemento de conjuntos
El complemento de u
conjunto X se forma con los elementos que le hacen falta al
conjunto X para ser igual al conjunto universal. Esto de representa
con Ac.
EJEMPLO:
Si el conjunto universal es U = { a, b, c, d, e } y A = { b, c, d }, entonces el complementario de A respecto de U está formado por los elementos del universal que no estén en A, esto es:
Al = { a, e }
Los conjuntos { a, e } y { b, c, d } son complementarios.
Unión e intersección de conjuntos
a Unión de dos o más conjuntos es el conjunto formado por todos los elementos que pertenecen a ambos conjuntos. La unión de A y B se denota 
. En diagramas se representan primero todos los elementos en sus respectivos conjuntos y luego se colorea todo el diagrama.
. En diagramas se representan primero todos los elementos en sus respectivos conjuntos y luego se colorea todo el diagrama.
La Intersección de dos o más conjuntos es el conjunto formado por los elementos que tienen en común ambos conjuntos. La intersección de A y B se denota 
. En diagramas se representan primero todos los elementos en sus respectivos conjuntos y luego se colorea la zona que pertenece a ambos conjuntos.
. En diagramas se representan primero todos los elementos en sus respectivos conjuntos y luego se colorea la zona que pertenece a ambos conjuntos.DIFERENCIA Y DIFERENCIA SIMÉTRICA ENTRE CONJUNTOS
ejemplo
En una visita que se hizo al Museo de Oro nos encontramos con un grupo de turistas estadounidenses. Clara, Raúl, Santiago, Érika, Claudia, Samuel y Sofía fueorn los guías. A nuestro grupo nos hablaban sólo en español y a los norteamericanos les hablaban solo en inglés.
Según el diagrama, ¿Quienes son los guías que solo hablan español?¿Quienes hablan solo ingles?¿Quienes son los guías que solo hablan ingles o español? Para entender las preguntas debemos hallar la diferencia y la diferencia simétrica de los conjuntos formados por los guías.
CONCEPTO:
- La diferencia de dos conjuntos A y B, "A - B", es el conjunto formado por los elementos que pertenecen al conjunto A y no pertenecen al conjunto B.
- La diferencia simétrica de dos conjuntos A y B , "A ∆ B", es el conjunto formado por todos los elementos que pertenecen a la unión de A y B y no pertenecen a la intersección entre A y B
Experimentos aleatorios
Un experimento aleatorio es aquél en el que si lo repetimos con las mismas condiciones iniciales no garantiza los mismos resultados. Así, por ejemplo, al lanzar una moneda no sabemos si saldrá cara o cruz, al lanzar un dado no sabemos qué número aparecerá, la extracción de las bolas de sorteos, loterías, etc. son experiencias que consideramos aleatorias puesto que en ellas no podemos predecir los resultados.
Espacio muestral
Al conjunto formado por todos los posibles resultados elementales de un experimento aleatorio se le denomina espacio muestral de dicho experimento.
Si consideramos como ejemplo el experimento consistente en el lanzamiento de una moneda:
En el siguiente vínculo puedes observar algunos ejemplos de espacios muestrales
- Los sucesos elementales son Cara (C) y Cruz (X).
- El espacio muestral asociado a dicho experimento es: E = {C, X}.
En el siguiente vínculo puedes observar algunos ejemplos de espacios muestrales
Sucesos y tipos de sucesos
Se denomina suceso a cualquier subconjunto de un espacio muestral, es decir, a cualquier posible resultado de un experimento aleatorio. Dentro de la gran generalidad que entraña esta definición, se pueden destacar algunos casos particulares de sucesos:
- Suceso seguro.
El suceso seguro es aquél que está formado por todos los resultados posibles del espacio muestral (E), es decir aquél que se realiza siempre. - Suceso imposible.
El suceso imposible es aquél que no ocurre nunca. Se expresa con el símbolo Ø. - Suceso elemental.
Un suceso se dice que es un suceso elemental si está formado por un único elemento del espacio muestral. - Suceso compuesto.
Un suceso se dice que es un suceso compuesto si está formado por más de un elemento del espacio muestral. - Suceso contrario o complementario
Se define el suceso contrario a A como el suceso que ocurre cuando no ocurre A. Puede notarse como:
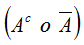
En la siguiente escena puedes observar como se construyen los espacios muestrales de algunos experimentos.
eventos
Primero necesitamos introdeucir algunos términos. Cuando trabajamos con probabilidad, una acción aleatoria o serie de acciones se llama experimento. Un resultado es la consecuencia de un experimento, y un eventoes una colección particular de resultados. Los eventos usualmente son descritos usando una característica común de los resultados.
Experimento
|
Resultados
|
Eventos
|
Lanzar un dado
|
Existen 6 resultados posibles:
{1, 2, 3, 4, 5, 6}
|
Sacar un número par: {2, 4, 6}
Sacar un 3: {3}
Sacar un 1 o un 3: {1, 3}
Sacar un 1 y un 3: { } (Sólo puede salir un número, por lo que esto es imposible. El event
o no contiene resultados.)
|
* evento simple es un evento con un solo resultado. Sacar un 1 sería un evento simple, porque existe sólo un resultado que funciona: 1. Sacar más que 5 también sería un evento simple, porque el evento incluye sólo al 6 como un resultado válido.
evento compuesto es un evento con más de
un resultado. Por ejemplo, lanzar un dado de 6 lados y sacar un número par: 2, 4, y 6.
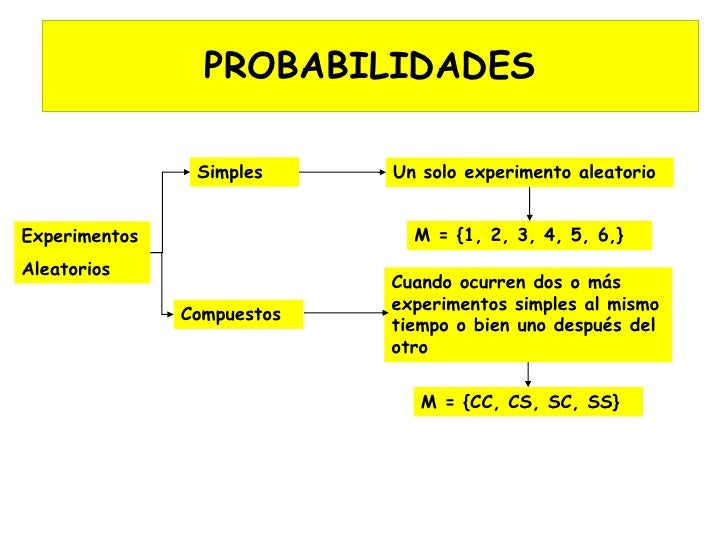
TÉCNICAS DE CONTEO
PRINCIPIO DE LA MULTIPLICACION
Si se desea realizar una actividad que consta de r pasos, en donde el primer paso de la actividad a realizar puede ser llevado a cabo de N1 maneras o formas, el segundo paso de N2 maneras o formas y el r-ésimo paso de Nr maneras o formas, entonces esta actividad puede ser llevada a efecto de. El principio multiplicativo implica que cada uno de los pasos de la actividad deben ser llevados a efecto, uno tras otro. Si un evento E1 puede suceder de n1 maneras diferentes, el evento E2 puede ocurrir de n2 maneras diferentes, y así sucesivamente hasta el evento Ep el cual puede ocurrir de np maneras diferentes, entonces el total de maneras distintas en que puede suceder el evento “ocurren E1 y E2…..y Ep” es igual a producto.
N1 x N2 x ..........x Nr maneras o formas
.- Calcular cuántos números enteros diferentes de tres dígitos se pueden formar con los dígitos 2,3,4,5,6,7,8 si los dígitos no pueden repetirse.
Solución:
Si es un número de tres dígitos, necesitamos un dígito para las centenas que puede ser cualquiera de los siete dígitos dados, después un dígito para las decenas que puede elegirse entre los seis dígitos restantes y finalmente el dígito de las unidades se
elegirá de los cinco últimos dígitos. Aplicando el Principio multiplicativo , tendremos:
PRINCIPIO DE PERMUTACION:
A diferencia de la formula de la multiplicación, se la utiliza para determinar el numero de posibles arreglos cuando solo hay un solo grupo de objetos. Permutación: un arreglos o posición de r objetos seleccionados de un solo grupo de n objetos posibles. Si nos damos cuenta los arreglos a, b, c y b, a, c son permutaciones diferentes, la formula que se utiliza para contar el numero total de permutaciones distintas es:
Donde: n= número total de objetos r= número de objetos seleccionados!= factorial, producto de los números naturales entre 1 y n.
NOTA: se puede cancelar números cuando se tiene las mismas cifras en numerador y denominador.
A diferencia de la formula de la multiplicación, se la utiliza para determinar el numero de posibles arreglos cuando solo hay un solo grupo de objetos. Permutación: un arreglos o posición de r objetos seleccionados de un solo grupo de n objetos posibles. Si nos damos cuenta los arreglos a, b, c y b, a, c son permutaciones diferentes, la formula que se utiliza para contar el numero total de permutaciones distintas es:
FÓRMULA: n P r = n! (n - r)
Ejemplo: ¿Como se puede designar los cuatro primeros lugares de un concurso, donde existen 15 participantes?
Aplicando la formula de la permutación tenemos:
Ejemplo: ¿Como se puede designar los cuatro primeros lugares de un concurso, donde existen 15 participantes?
Aplicando la formula de la permutación tenemos:
n P r = n! (n - r)! = 15! = 15*14*13*12 *11*10*9*8*7*6*5*4*3*2*1 (15-4)! 11*10*9*8*7*6*5*4*3*2*1 = 32760
NOTA: se puede cancelar números cuando se tiene las mismas cifras en numerador y denominador.
PRINCIPIO DE COMBINACION:
En una permutación, el orden de los objetos de cada posible resultado es diferente. Si el orden de los objetos no es importante, cada uno de estos resultados se denomina combinación. Por ejemplo, si se quiere formar un equipo de trabajo formado por 2 personas seleccionadas de un grupo de tres (A, B y C). Si en el equipo hay dos funciones diferentes, entonces si importa el orden, los resultados serán permutaciones. Por el contrario si en el equipo no hay funciones definidas, entonces no importa el orden y los resultados serán combinaciones. Los resultados en ambos casos son los siguientes:Permutaciones: AB, AC, BA, CA, BC, CBCombinaciones: AB, AC, BCCombinaciones: Es el número de formas de seleccionar r objetos de un grupo de n objetos sin importar el orden.La fórmula de combinaciones es: n C r = n! r! (n – r)!Ejemplo: En una compañía se quiere establecer un código de colores para identificar cada una de las 42 partes de un producto. Se quiere marcar con 3 colores de un total de 7 cada una de las partes, de tal suerte que cada una tenga una combinación de 3 colores diferentes. ¿Será adecuado este código de colores para identificar las 42 partes del producto?Usando la fórmula de combinaciones:n C r = n! = 7! = 7! = 35 r! (n – r )! 3! (7 – 3)! 3! 4!El tomar tres colores de 7 posibles no es suficiente para identificar las 42 partes del producto.
2.un experimento consiste en lanzar al aireen forma simultanea tres monedas y observar el resultado de los lados superiores. construir el espacio muestra.
S={(c,c,c),(c,c,s),(c,sc),(s,s,c)}
(s,c,c),(s,s,c),(s,c,s),(s,s,
3.un experimento consiste en lanzar simultáneamente dos dados y observar el resultado. construir el espacio muestra.
determinar el espacio muestral.
(1,1),(1,2),(1,3),(1,4),(1,5),(1,6)
(2,1),(2,2),(2,3),(2,4),(2,5),(2,6)
(3,1),(3,2),(3,3),(3,4),(3,5),(3,6)
(4,1),(4,2),(4,3),(4,4),(4,5),(4,6)
(5,1),(5,2),(5,3),(5,4),(5,5),(5,6)
(6,1),(6,2),(6,3),(6,4),(6,5),(6,6)
4.experimento: saca una carta de una baraja de poquer que contiene 52 cartas.
a. escribir los elementos del evento que consiste en obtener un as.
♡ corazón A 2.3.4......jqk 13
♢ picas A 2.3.4........jqk....13
♣ diamantes A 2.3.4........jqk....13
♠ trebol A 2.3.4........jqk....13
______ 52
las posibilidades de un as son 4.
b. escribir los elementos del evento que consiste en obtener una Q roja.
corazón ❤
2 posibles que salga roja
pikas ♤
c. escribir los elementos del evento que consiste en obtener una carta roja.
corazon ❤ A 2,3,4,5,6,7,8,9, J;Q;K >13
diamante ♦ B 2,3,4,5,6,7,8,9, J;Q;k >13
_______
26
5. se lanza una moneda 2 veces ¿cual es la probabilidad de obtener 2 sellos?.
{ (c,c) , (c,s) , (s,c) , (s,s) } la probabilidad de obtener 2 sellos es de 1/4
P(S,S) 1/4 =0.25 =25%
6. se lanza una vez una moneda y un dado ¿cual es la probabilidad de obtener cara en la moneda yy un numero par en el dado?.
moneda P(C)= 1/2 =0.5
dado par P(P)= 3/6=0.5
P(C∩P) = D(C).D(D)
=(0.5).(0.5)
=0.5
7. encuentra la probabilidad que existe de que al lanzar dos dados las sumas de las caras sea igual a 7?
S= 6 OPCIONES
P = (s) = 6/36 =1/16 =16.66%
LA PROBABILIDAD QUE LA SUMA SEA 7 ES DE 16.66%
8.cual es la probabilidad que existe que al seleccionar aleatoria mente un día del presente mes, este sea un lunes?
LUNES DEL MES = 4
DIAS AL MES =30
=4/30= 0.13= 13%
9.utilizando los postulados de la probabilidad
- p(A)>0,
- p(S)=1
- p(AUB)=P(A)+P(B)
realizar:
a. una maquina automática llena de bolsas de plástico con una mezcla de frijoles, brocolis y otras legumbres. la mayoría de bolsas contiene el peso correcto.
pero debido a ligeras variaciones en el tamaño de los frijoles y las otras legumbres,un paquete puede tener un peso ligeramente menor o mayor. una verificación de 1000 paquetes indico el los siguientes resultados:
peso numero de paquetes probabilidad
con peso menor 25 0.025
con peso correcto 900 0.900
con peso mayor 75 0.075
total 1000 1.00
cual es la probabilidad que tenga un peso mayor o menor?
a. evento que sea menor
b. evento que sea correcto
c. evento que sea mayor
LA PROBABILIDAD QUE TENGA UN PESO MAYOR O MENOR ES DEL 10%.
b. de los estudiantes de una faculta de derecho 30% son de primer año,35% de segundo,20% de tercero,10% de cuarto y el resto de quinto. si uno de eso alumnos se gano 10 millones de pesos.¿cual es la probabilidad que el alumno sea de primero o de segundo año?
año estudiante %
1 0.3 30%
2 0.35 35%
3 0.20 20%
4 0.10 5%
5 0.5
P(AUB)= P(A)+P(B)
=0.3+0.35
=0.65
=65% la probabilidad que el alumno sea de primero o segundo año es del 65%.
c. la de que 0.1.2.3.4. o mas clientes pidan determinado articulo de los estantes en un supermercado cierto día son,respectivamente, 0.10,0.40,0.30,.015, y 0.05 determine la probabilidad de que:
1. ninguno o un cliente pida el articulo
2.almenos dos clientes pidan el articulo
3. a lo sumo tres clientes pidan el articulo
4.al menos un cliente pida el articulo
cliente
0 0.10
1 0.40
2 0.30
3 0.15
4 0.05
1
1. P(X=0) +P(X=1)
=0.10+0.40
=0.50
=50%
2. P=(ALMENOS 2)
P=(X>2)
=1- [P(X<2) ]
=1- [ P(X=0)+P(X=1) ]
=1-0.5
=0.5
3. P( a lo sumo tres)= P(x<3)
=1-P(x>4)
=1-0.05
=0.95
4. al menos 1
=1- P(x=0)
=1- 0.10
=0.90
1)
Si se
elige un cliente habitual cual es la probabilidad de que haya pagado a crédito.
Solución
A Ç B = {ser crédito o contado}
p(A|B) = 0,70/0,50 = 1,4 la probabilidad es 1,4 que haga la compra a crédito.
A1 = {0,4 }; A2 =
{0,3}; A3 = {0,2.}
3) En un almacén se hace una promoción de
llantas nacionales 58 y importadas 75 cuan es la probabilidad de comprar
importada.
Solución:
P(A/D)
= 75 = 1,29 compraron llantas importadas
EJEMPLO
Un médico cirujano se especializa en cirugías estéticas. Entre sus pacientes, el 20% se realizan correcciones faciales, un 35% implantes mamarios y el restante en otras cirugías correctivas. Se sabe además, que son de genero masculino el 25% de los que se realizan correcciones faciales, 15% implantes mamarios y 40% otras cirugías correctivas. Si se selecciona un paciente al azar, determine:
a. Determine la probabilidad de que sea de género masculino
b. Si resulta que es de género masculino, determine la probabilidad que se haya realizado una cirugía de implantes mamarios.
SOLUCIÓN:
Se definen los sucesos:
Suceso F: pacientes que se realizan cirugías faciales
Suceso M: pacientes que se realizan implantes mamarios
Suceso O: pacientes que se realizan otras cirugías correctivas
Suceso H: pacientes de género masculino
a. La probabilidad de que sea de género masculino se refiere a un problema de probabilidad total, ya que es el suceso condicionado y las cirugías los condicionantes. Dicho valor será:
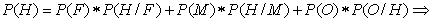b. Como el suceso condicionado ha ocurrido entonces se aplica el teorema de bayes, luego, el valor de la probabilidad será:
EJEMPLO
Un Doctor dispone de tres equipos electrónicos para realizar ecosonogramas. El uso que le da a cada equipo es de 25% al primero, 35% el segundo en y 40% el tercero. Se sabe que los aparatos tienen probabilidades de error de 1%, 2% y 3% respectivamente. Un paciente busca el resultado de una ecografía y observa que tiene un error. Determine la probabilidad de que se ha usado el primer aparato.
SOLUCIÓN:
Se definen los sucesos:
Suceso P: seleccionar el primer aparato
Suceso S: seleccionar el segundo aparato
Suceso T: seleccionar el tercer aparato
Suceso E: seleccionar un resultado con error
Se puede observar que la pregunta es sobre determinar la probabilidad de que un examen errado sea del primer aparato, es decir, ya ha ocurrido el error. Por lo tanto, debemos recurrir al teorema de bayes. Claro está, que es necesario de igual forma obtener la probabilidad de que los aparatos produzcan un resultado erróneo, por lo tanto:
video de ejercicio teorema de bayes
En una permutación, el orden de los objetos de cada posible resultado es diferente. Si el orden de los objetos no es importante, cada uno de estos resultados se denomina combinación. Por ejemplo, si se quiere formar un equipo de trabajo formado por 2 personas seleccionadas de un grupo de tres (A, B y C). Si en el equipo hay dos funciones diferentes, entonces si importa el orden, los resultados serán permutaciones. Por el contrario si en el equipo no hay funciones definidas, entonces no importa el orden y los resultados serán combinaciones. Los resultados en ambos casos son los siguientes:Permutaciones: AB, AC, BA, CA, BC, CBCombinaciones: AB, AC, BCCombinaciones: Es el número de formas de seleccionar r objetos de un grupo de n objetos sin importar el orden.La fórmula de combinaciones es: n C r = n! r! (n – r)!Ejemplo: En una compañía se quiere establecer un código de colores para identificar cada una de las 42 partes de un producto. Se quiere marcar con 3 colores de un total de 7 cada una de las partes, de tal suerte que cada una tenga una combinación de 3 colores diferentes. ¿Será adecuado este código de colores para identificar las 42 partes del producto?Usando la fórmula de combinaciones:n C r = n! = 7! = 7! = 35 r! (n – r )! 3! (7 – 3)! 3! 4!El tomar tres colores de 7 posibles no es suficiente para identificar las 42 partes del producto.
2.un experimento consiste en lanzar al aireen forma simultanea tres monedas y observar el resultado de los lados superiores. construir el espacio muestra.
S={(c,c,c),(c,c,s),(c,sc),(s,s,c)}
(s,c,c),(s,s,c),(s,c,s),(s,s,
3.un experimento consiste en lanzar simultáneamente dos dados y observar el resultado. construir el espacio muestra.
determinar el espacio muestral.
(1,1),(1,2),(1,3),(1,4),(1,5),(1,6)
(2,1),(2,2),(2,3),(2,4),(2,5),(2,6)
(3,1),(3,2),(3,3),(3,4),(3,5),(3,6)
(4,1),(4,2),(4,3),(4,4),(4,5),(4,6)
(5,1),(5,2),(5,3),(5,4),(5,5),(5,6)
(6,1),(6,2),(6,3),(6,4),(6,5),(6,6)
4.experimento: saca una carta de una baraja de poquer que contiene 52 cartas.
a. escribir los elementos del evento que consiste en obtener un as.
♡ corazón A 2.3.4......jqk 13
♢ picas A 2.3.4........jqk....13
♣ diamantes A 2.3.4........jqk....13
♠ trebol A 2.3.4........jqk....13
______ 52
las posibilidades de un as son 4. b. escribir los elementos del evento que consiste en obtener una Q roja.
corazón ❤
2 posibles que salga roja
pikas ♤
las posibilidades de un as son 4. b. escribir los elementos del evento que consiste en obtener una Q roja.
corazón ❤
2 posibles que salga roja
pikas ♤
c. escribir los elementos del evento que consiste en obtener una carta roja.
corazon ❤ A 2,3,4,5,6,7,8,9, J;Q;K >13
diamante ♦ B 2,3,4,5,6,7,8,9, J;Q;k >13
_______
26
5. se lanza una moneda 2 veces ¿cual es la probabilidad de obtener 2 sellos?.
{ (c,c) , (c,s) , (s,c) , (s,s) } la probabilidad de obtener 2 sellos es de 1/4
P(S,S) 1/4 =0.25 =25%
6. se lanza una vez una moneda y un dado ¿cual es la probabilidad de obtener cara en la moneda yy un numero par en el dado?.
moneda P(C)= 1/2 =0.5
dado par P(P)= 3/6=0.5
P(C∩P) = D(C).D(D)
=(0.5).(0.5)
=0.5
7. encuentra la probabilidad que existe de que al lanzar dos dados las sumas de las caras sea igual a 7?
S= 6 OPCIONES
P = (s) = 6/36 =1/16 =16.66%
LA PROBABILIDAD QUE LA SUMA SEA 7 ES DE 16.66%
8.cual es la probabilidad que existe que al seleccionar aleatoria mente un día del presente mes, este sea un lunes?
LUNES DEL MES = 4
DIAS AL MES =30=4/30= 0.13= 13%
9.utilizando los postulados de la probabilidad
- p(A)>0,
- p(S)=1
- p(AUB)=P(A)+P(B)
realizar:
a. una maquina automática llena de bolsas de plástico con una mezcla de frijoles, brocolis y otras legumbres. la mayoría de bolsas contiene el peso correcto.
pero debido a ligeras variaciones en el tamaño de los frijoles y las otras legumbres,un paquete puede tener un peso ligeramente menor o mayor. una verificación de 1000 paquetes indico el los siguientes resultados:
peso numero de paquetes probabilidad
con peso menor 25 0.025
con peso correcto 900 0.900
con peso mayor 75 0.075
total 1000 1.00
cual es la probabilidad que tenga un peso mayor o menor?
a. evento que sea menor
b. evento que sea correcto
c. evento que sea mayor
LA PROBABILIDAD QUE TENGA UN PESO MAYOR O MENOR ES DEL 10%.
b. de los estudiantes de una faculta de derecho 30% son de primer año,35% de segundo,20% de tercero,10% de cuarto y el resto de quinto. si uno de eso alumnos se gano 10 millones de pesos.¿cual es la probabilidad que el alumno sea de primero o de segundo año?
año estudiante %
1 0.3 30%
2 0.35 35%
3 0.20 20%
4 0.10 5%
5 0.5
P(AUB)= P(A)+P(B)
=0.3+0.35
=0.65
=65% la probabilidad que el alumno sea de primero o segundo año es del 65%.
c. la de que 0.1.2.3.4. o mas clientes pidan determinado articulo de los estantes en un supermercado cierto día son,respectivamente, 0.10,0.40,0.30,.015, y 0.05 determine la probabilidad de que:
1. ninguno o un cliente pida el articulo
2.almenos dos clientes pidan el articulo
3. a lo sumo tres clientes pidan el articulo
4.al menos un cliente pida el articulo
cliente
0 0.10
1 0.40
2 0.30
3 0.15
4 0.05
1
1. P(X=0) +P(X=1)=0.10+0.40
=0.50
=50%
2. P=(ALMENOS 2)
P=(X>2)
=1- [P(X<2) ]
=1- [ P(X=0)+P(X=1) ]
=1-0.5
=0.5
3. P( a lo sumo tres)= P(x<3)
=1-P(x>4)
=1-0.05
=0.95
4. al menos 1
=1- P(x=0)
=1- 0.10
=0.90
1)
Si se
elige un cliente habitual cual es la probabilidad de que haya pagado a crédito.
Solución
A = {ser crédito} B = {ser contado}
A Ç B = {ser crédito o contado}
p(A|B) = 0,70/0,50 = 1,4 la probabilidad es 1,4 que haga la compra a crédito.
A Ç B = {ser crédito o contado}
p(A|B) = 0,70/0,50 = 1,4 la probabilidad es 1,4 que haga la compra a crédito.
2)
Un
inversionista compra tres acciones 0,4-0,3-0,2 cuál es la probabilidad que
aumenten su valor.
A1 = {0,4 }; A2 =
{0,3}; A3 = {0,2.}
p(A1) = 0,4;
p(A2|A1) = 0,3 p(A3|A1 Ç A2) = 0,1
p (A1 Ç A2 Ç A3) =
0,4 x 0,3 x 0,2 = 0,024. Esta es la probabilidad de que aumenten.
3) En un almacén se hace una promoción de
llantas nacionales 58 y importadas 75 cuan es la probabilidad de comprar
importada.
Solución:
P(A/D)
= 75 = 1,29 compraron llantas importadas
---------
EJEMPLO
Un médico cirujano se especializa en cirugías estéticas. Entre sus pacientes, el 20% se realizan correcciones faciales, un 35% implantes mamarios y el restante en otras cirugías correctivas. Se sabe además, que son de genero masculino el 25% de los que se realizan correcciones faciales, 15% implantes mamarios y 40% otras cirugías correctivas. Si se selecciona un paciente al azar, determine:
a. Determine la probabilidad de que sea de género masculino
b. Si resulta que es de género masculino, determine la probabilidad que se haya realizado una cirugía de implantes mamarios.
SOLUCIÓN:
Se definen los sucesos:
Suceso F: pacientes que se realizan cirugías faciales
Suceso M: pacientes que se realizan implantes mamarios
Suceso O: pacientes que se realizan otras cirugías correctivas
Suceso H: pacientes de género masculino
a. La probabilidad de que sea de género masculino se refiere a un problema de probabilidad total, ya que es el suceso condicionado y las cirugías los condicionantes. Dicho valor será:
b. Como el suceso condicionado ha ocurrido entonces se aplica el teorema de bayes, luego, el valor de la probabilidad será:
EJEMPLO
Un Doctor dispone de tres equipos electrónicos para realizar ecosonogramas. El uso que le da a cada equipo es de 25% al primero, 35% el segundo en y 40% el tercero. Se sabe que los aparatos tienen probabilidades de error de 1%, 2% y 3% respectivamente. Un paciente busca el resultado de una ecografía y observa que tiene un error. Determine la probabilidad de que se ha usado el primer aparato.
SOLUCIÓN:
Se definen los sucesos:
Suceso P: seleccionar el primer aparato
Suceso S: seleccionar el segundo aparato
Suceso T: seleccionar el tercer aparato
Suceso E: seleccionar un resultado con error
Se puede observar que la pregunta es sobre determinar la probabilidad de que un examen errado sea del primer aparato, es decir, ya ha ocurrido el error. Por lo tanto, debemos recurrir al teorema de bayes. Claro está, que es necesario de igual forma obtener la probabilidad de que los aparatos produzcan un resultado erróneo, por lo tanto:
video de ejercicio teorema de bayes
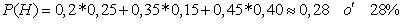
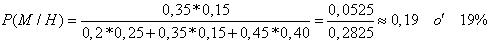
No hay comentarios.:
Publicar un comentario