estadística de la probabilidad

ESTADÍSTICA DE LA PROBABILIDAD

Maria Johanna Angulo

Marta liliana Muñoz 

Contaduría Publica

¿Qué es un diagrama de árbol?

El diagrama de árbol es una representación gráfica de los posibles resultados del experimento, el cual consta una serie de pasos, donde cada uno de los pasos tiene un número finito de maneras de ser llevado a cabo.

Se utiliza en los problemas de conteo y probabilidad.

¿Para qué sirve?

• Un diagrama de árbol es un método gráfico para identificar todas las partes necesarias para  alcanzar algún objetivo final

• Se emplea para descomponer una meta u objetivo en una serie de actividades que deban o puedan  hacerse. A través de la representación gráfica de actividades se facilita el entendimiento de las  acciones que intervendrán

• Permite a los miembros del equipo de trabajo  expandir su pensamiento al crear soluciones sin  perder de vista el objetivo principal o los objetivos secundarios

• Ubica al equipo para que se dirija a situaciones reales versus teóricas.

Cómo se elabora

• Establezca el objetivo que se analizará a través del diagrama de árbol. Es muy importante  que el objetivo quede  claro  para  todos  y   que    esté    expresado    de  manera  activa.
• Arme el equipo adecuado. Se sugiere un equipo de 4 a 8 participantes. Considere   que   aquellos   que seleccione   deberán   estar   involucrados   en la problemática a fondo para aportar soluciones y que el diagrama de árbol cuente así con los niveles de análisis necesarios.
• Genere el mayor número posible de “cabeceras del diagrama de árbol” Esto es las ideas o sub-objetivos hacia los que se enfocarán las acciones para lograr el objetivo   principal.
• Descomponga cada “cabecera” o título principal en mayor  detalle.  Vaya  acomodando  las  ideas  por subtemas llegando a tres o cuatro niveles.
• Detenga la descomposición de temas cuando ya se perfilen tareas específicas a realizarse.
• Revise el diagrama de árbol. Asegúrese de que tiene un flujo lógico y que esté lo más completo posible.
• Pregunte al equipo si observa algún punto que sea muy obvio y se haya olvidado incluir.
• Pregúntese junto con el equipo si las tareas  resultantes son necesarias para lograr el objetivo.

Ventajas

• Exhorta a los integrantes del equipo a ampliar su modo de pensar al crear soluciones.
• Mantiene a todo el equipo vinculado a las metas y sub metas generales de una tarea.
• Mueve al equipo de planificación de la teoría al mundo real.

Beneficios

• Permite obtener una visión de conjunto del objeto de estudio.
• Permite identificar los medios necesarios para alcanzar una meta o resolver un problema.
• Permite identificar las causas primarias y secundarias de un problema y asignar prioridades al momento de resolver un problema.
• Permite entender la relación causa – efecto de los problemas.
• Permite identificar los objetivos las metas de cada tarea.

Fuentes: wikipedia.org / dgplades.salud.gob.mx / aiteco.com / articulo.org

Principio de la multiplicación.

“Si un suceso se puede realizar de “m” formas diferentes y luego se puede realizar otro suceso de “n” formas diferentes, el número total de formas en que pueden  el otro. El “y” indica multiplicación.

Ejemplo: ¿de cuántas formas se puede vestir una persona que tiene 3 pantalones y 3 camisas?

Para vestirse, la persona se pone el pantalón y luego la camisa, es decir tiene 3 x 3 = 9 opciones diferentes de vestirse.

   

Principio aditivo

Si se desea llevar a efecto una actividad, la cuál tiene formas alternativas para ser realizada, donde la primera de esas alternativas puede ser realizada de M maneras o formas, la segunda alternativa puede realizarse de N maneras o formas ..... y la última de las alternativas puede ser realizada de W maneras o formas, entonces esa actividad puede ser llevada  a cabo de,

                        M + N + .........+ W  maneras o formas

Ejemplos:

1)      Una persona desea comprar una lavadora de ropa, para lo cuál ha pensado que puede seleccionar de entre las marcas Whirpool, Easy y General Electric, cuando acude a hacer la compra se encuentra que la lavadora de la marca W se presenta en dos tipos de carga ( 8 u 11 kilogramos), en cuatro colores diferentes y puede ser automática o semiautomática, mientras que la lavadora de la marca E, se presenta en tres tipos de carga (8, 11 o 15 kilogramos), en dos colores diferentes y puede ser automática o semiautomática y la lavadora de la marca GE, se presenta en solo un tipo de carga, que es de 11 kilogramos, dos colores diferentes y solo hay semiautomática. ¿Cuántas maneras tiene esta persona de comprar una lavadora?

Solución:

Suponga que un salón de clase está constituido por 35 alumnos.

a) El maestro desea que tres de los alumnos lo ayuden en actividades tales como mantener el aula limpia o entregar material a los alumnos cuando a

M = Número de maneras de seleccionar una lavadora Whirpool

N = Número de maneras de seleccionar una lavadora de la marca Easy

W = Número de maneras de seleccionar una lavadora de la marca General Electric

M = 2 x 4 x 2 = 16 maneras

N = 3 x 2 x 2 = 12 maneras

W = 1 x 2 x 1 = 2 maneras

 M + N + W = 16 + 12 + 2 = 30 maneras de seleccionar una lavadora

Permutaciones

Para entender lo que son las permutaciones es necesario definir lo que es una combinación y lo que es una permutación para establecer su diferencia y de esta manera entender claramente cuando es posible utilizar una combinación y cuando utilizar una permutación al momento de querer cuantificar los elementos de algún evento.

sí sea necesario.

b) El maestro desea que se nombre a los representantes del salón (Presidente, Secretario y Tesorero).

Solución:

a)      Suponga que por unanimidad se ha elegido a Daniel, Arturo y a Rafael para limpiar el aula o entregar material, (aunque pudieron haberse seleccionado a Rafael, Daniel y a Enrique, o pudo haberse formado cualquier grupo de tres personas para realizar las actividades mencionadas anteriormente).

¿Es importante el orden como se selecciona a los elementos que forma el grupo de tres personas?

Reflexionando al respecto nos damos cuenta de que el orden en este caso no tiene importancia, ya que lo único que nos interesaría es el contenido de cada grupo, dicho de otra forma, ¿quiénes están en el grupo? Por tanto, este ejemplo es una combinación, quiere decir esto que las combinaciones nos permiten formar grupos o muestras de elementos en donde lo único que nos interesa es el contenido de los mismos

.

b)      Suponga que se han nombrado como representantes del salón a Daniel como Presidente, a Arturo como secretario y a Rafael como tesorero, pero resulta que a alguien se le ocurre hacer algunos cambios, los que se muestran a continuación:

Combinaciones

Como ya se mencionó anteriormente, una combinación, es un arreglo de elementos en donde no nos interesa el lugar o posición que ocupan los mismos dentro del arreglo. En una combinación nos interesa formar grupos y el contenido de los mismos.

La fórmula para determinar el número de combinaciones es:

Ejemplo:

1)      a. Si se cuenta con 14 alumnos que desean colaborar en una campaña pro limpieza del Tec, cuantos grupos de limpieza podrán formarse si se desea que consten de 5 alumnos cada uno de ellos, b.si entre los 14 alumnos hay 8 mujeres, ¿cuantos de los grupos de limpieza tendrán a 3 mujeres?, c.¿cuántos de los grupos de limpieza contarán con 4 hombres por lo menos?

Solución:

a. n = 14,  r = 5

                                           14C5 = 14! / (14 - 5 )!5! = 14! / 9!5!

                                         = 14 x 13 x 12 x 11 x 10 x 9!/ 9!5!

                                         = 2002 grupos

Entre los 2002 grupos de limpieza hay grupos que contienen solo hombres, grupos que contienen solo mujeres y grupos mixtos, con hombres y mujeres.

b. n = 14 (8 mujeres y 6 hombres),           r = 5

probabilidades

1.  un estudio sobre los gustos musicales de los estudiantes en una universidad se encuesto un total de 70 estudiantes quienes  manifestaron sus gustos de la siguiente manera:

20 la música salsa

23 rock

40 baladas

10 baladas y salsa

13 baladas y rock

5 rock y salsa

3 rock , salsa, baladas

diagrama de venn

70

2. Un producto se arma en tres etapas  en la primera etapa hay 5 líneas de armado en la segunda 4 líneas,  En la tercera  6 líneas  ¿de cuantas formas puede moverse el producto en el proceso  de armado?

principio de la  multiplicación

5*4*6=120

3.en Colombia las placas de los carros están formadas por tres números  y tres  letras :

a. ¿cuántas placas se pueden generar en estas condiciones?  Se puede escoger de 10 maneras diferentes  así que :

3 números  10*10*10=

1000

3 letras  26 maneras diferentes 26*26*26=

17576

17576*1000=

17576000

b. En este experimento es válido hablar de orden de muestra?

c. en caso que para una ciudad como Medellín se asignen solamente las placas cuya primera letra es m o n ¿cuántos automóviles pueden estar matriculados en Medellín?

Las letras serian 24 entonces se dice que:

24*24*24 = 13824 + 1000 = 13824000.

4 . un vendedor de automóviles nuevos quiere impresionar  a sus clientes potenciales  con la cantidad posible de diferentes combinaciones  de que se disponen  un modelo presenta tres tipos de motores, dos trasmisiones ,  cinco colores de carrocería  y dos colores de interiores, ¿Cuántas posibilidades de elecciones  existen  respecto a estas opciones?.

Se toman todas las opciones y se aplica  el  principio de la multiplicación

3 tipos de motores *  2 trasmisiones* 5 colores de carrocerías* 2 colores de interiores  = 60 serian la cantidad de muestras.

5.  explique la diferencia entre:

PERMUTACIONES	COMBINACIONES
*si importa el orden	* no importa el orden
Calcula las posibles agrupaciones que se pueden establecer con todos los elementos de un grupo, por lo tanto, lo que diferencia a cada subgrupo del resto es el orden de los elementos	Determina el número de subgrupos de 1, 2, 3, etc. elementos que se pueden formar con los "n" elementos de una nuestra
"La combinación de la cerradura es 472": ahora sí importa el orden. "724" no funcionaría, ni "247". Tiene que ser exactamente 4-7-2. Así que en matemáticas usamos un lenguaje más preciso: Una permutación es una combinación ordenada.	"Mi ensalada de frutas es una combinación de manzanas, uvas y bananas": no importa en qué orden pusimos las frutas, podría ser "bananas, uvas y manzanas" o "uvas, manzanas y bananas", es la misma ensalada.

http://www.disfrutalasmatematicas.com/combinatoria/combinaciones-permutaciones.html

6. se juegan 5 dados  ¿de cuantas maneras pueden caer?

7.si un conjunto  tiene 10 elementos, ¿Cuántos subconjuntos de 2 electos puedes formar si el orden en aparece en los 2 elementos tiene importancia.

8) en un concurso de belleza se suele escoger 15 sefinalistas y luego se escogen 5 finalistas de cuantas diferentes formas se pueden ocupar 5 primeros puestos.

Solución:

Multiplicación de opciones.

Dando que M=15 Y N=5, hay 15*5=75 maneras distintas en que se pueden elegir las 5 finalistas.

9) una liga de futbol está integrada por 6 equipos, cuantos resultados diferentes posibles habrán en una temporada supón que ningún equipo terminada empatado con el otro.

SOLUCIÓN:

Puesto que n1=n2=n3=n4=n5=n6 en total hay.

6.6.6.6.6.6= 46656 posibilidades de resultados diferentes en la liga.

10. la junta de una compañía ABC ESTA COMPUESTA por 15 miembros de cuanta maneras se puede elegir un vicepresidente, presidente y secretario.

 Dando que M=15 Y N=3, hay 15*3=45 maneras distintas en que se pueden elegir las un presidente, vicepresidente y un secretario.

11. se va a elegir un comité de 5 miembros entre un grupo de 7 candidatos de cuantas formas se puede hacer esto, si los 7 candidatos van a ocupar puestos diferentes. De cuantas maneras pueden ocupar estos puestos.

Solución 

Puesto que n1= y n=7, hay 5*7= 35 formas de elegir 5 miembros del comité

12. en una clase de estadística hay 30 estudiantes 24 hombres y 6 mujeres de cuantas maneras se puede constituir un comité de cuatro estudiantes de cuantas maneras si debe haber 2 mujeres en el comité.

Solución 

30 hombres dando que n1=30,n2=29, n3= 28 sin importar el orden a quien elija hay 30*29*28=24.360 posibilidades distintas.

6 mujeres dando que n1=6,n2=5,=4 sin importar el orden a quien elija hay 6*2= 12 posibilidades distintas.

13 un estudiante tiene 7 libros que quiere colocar en su biblioteca sin embargo solo caben 4 cuantas maneras existen para colocar solo 4 libros

Solución 

Dado que M=7 Y N=4 HAY 7*4= 28 maneras diferentes de colocar los libros en la biblioteca.

Definir y dar ejemplos:

Conjuntos

 Conjunto (del latín coniunctus) es lo que está unido, contiguo o incorporado a otra cosa, o que se encuentra mezclado, combinado o aliado con otra cosa diversa. Un conjunto, por lo tanto, es un agregado  varias cosas o personas.

Ejemplo

Conjunto de los números primos”.

El conjunto de las vocales.


: http://definicion.de/conjunto/#ixzz4QOkSbU4V

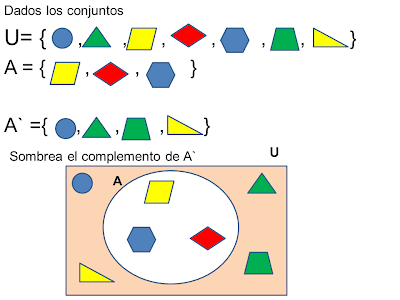
Complemento de conjuntos

El complemento de u conjunto X se forma con los elementos   que le hacen falta al conjunto  X  para ser igual al conjunto universal. Esto de representa con A^c.

EJEMPLO: 

 http://matematicasquinto3.webnode.com.co/news/diferencia-de-conjuntos/

Unión e intersección de conjuntos

diferencia de conjuntos

Sean A y B conjuntos. La diferencia del conjunto A menos B, denotado por A –  B, es el conjunto formado por los elementos que estén en  A y no en  B. ejemplo.